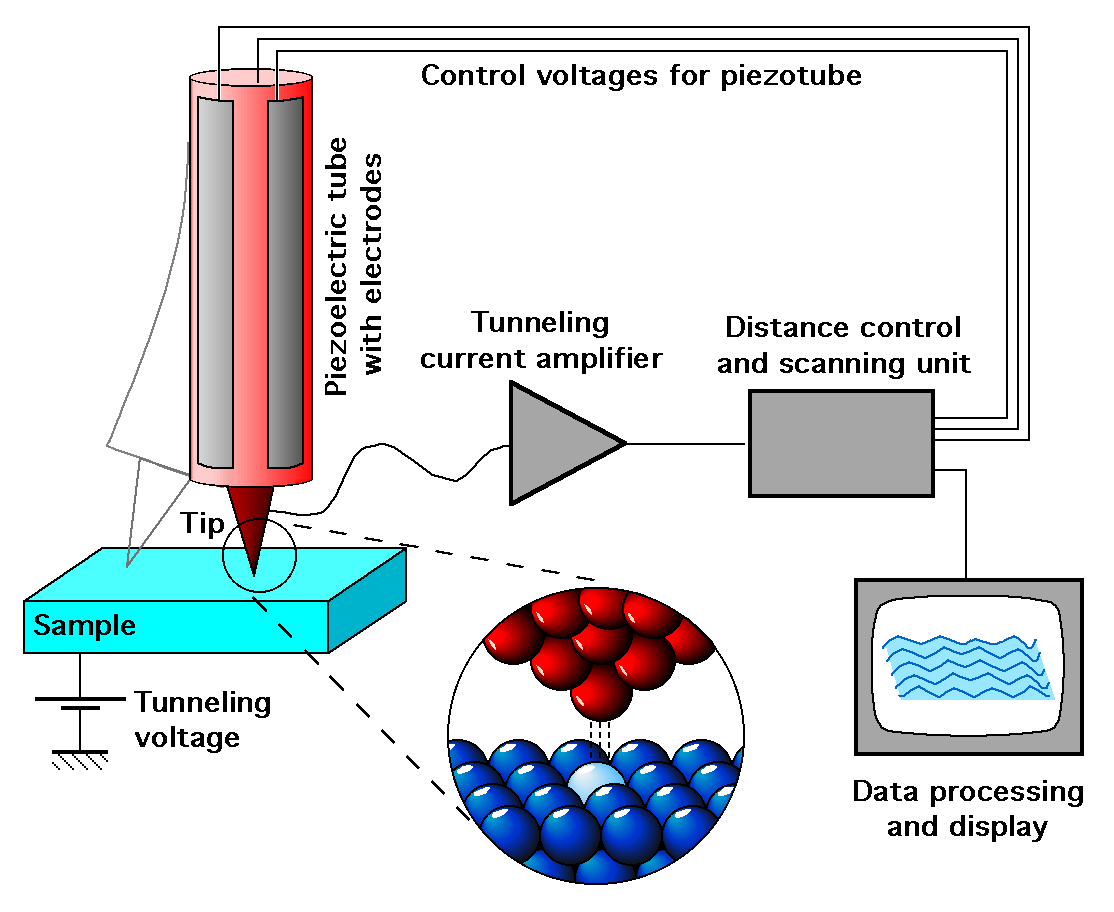
Feedback Loop
Using Ref. \cite{optimalConditionsForSTMTheory} we can describe the STM feedback loop as
The parameter $\alpha$ is defined as: \begin{equation} \alpha= 1.025 K_L log_{10}(e) \sqrt{\phi} \end{equation} where $K_L$ is the conversion factor of the logarithmic amplifier (in fl_K1s), and $\phi$ the average barrier height (in eV). The total gain of the closed loop can be defined as \begin{equation} G_0=\alpha A \gamma_0 G_1 \end{equation} where $\gamma_0$ is the voltage sensitivity constant. We can define the following adimensional terms: \begin{equation} G= G_0 G_2 \end{equation} \begin{equation} K= \frac{G_0 K_1}{\omega_s} \end{equation} \begin{equation} \tau_s= \omega_s \tau \end{equation} \begin{equation} W_0= \frac{\omega_0}{\omega_s} \end{equation} According to \cite{optimalConditionsForSTMTheory} (https://doi.org/10.1063/1.1149191), the stability condition is \begin{equation} K< W_0^2 \tau_s(1-G) \end{equation} the amplitude conditions are \begin{equation} K \geq \sqrt{\frac{G^2-(1+\Delta)^2 (1-G)^2}{(1+\Delta)^2-1}} \ \ \ \mbox{for}\Delta>0 \end{equation} \begin{equation} K \geq \sqrt{\frac{-G^2+(1+\Delta)^2 (1-G)^2}{(1+\Delta)^2-1}} \ \ \ \mbox{for}\Delta < 0 \end{equation} the phase shift condition can be obtained from \begin{equation} \tan{\phi_s}=\frac{K}{G(1-G)-K^2} \end{equation} which means... \begin{equation} K=\frac{-1}{2 \tan{\phi_s}} \pm \sqrt{\frac{1}{4 \tan{\phi_s}^2}+G(1-G)} \end{equation}
The optimal area for imaging is shown in the following plot as a shadowed area, constrained by the combination of limits described above

*The limits for the amplitude condition below are not the same as the ones shown in the plot above, still need to find why !